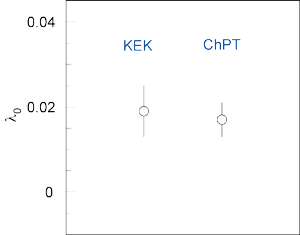
The theory of hadron interaction is quantum chromodynamics (QCD). However, at low energies perturbative methods cannot be applied since the coupling constant becomes very large. One method uses a low energy effective model, Chiral Perturbation Theory (CHPT), which is a rigorous methodology for QCD in the low-energy regions. The predictive power of ChPT can be stringently tested by the form factors of the simplest semileptonic decay Kl3[1]. For the calculation of the Kl3 form factors, a parameterization in terms of the form factors f+ and f0 which are associated with vector and scalar exchange, respectively, are convenient. The form factor f0 is related to f+ and f- through